Scheduling (production processes)
Scheduling is an important tool for manufacturing and engineering, where it can have a major impact on the productivity of a process. In manufacturing, the purpose of scheduling is to minimize the production time and costs, by telling a production facility when to make, with which staff, and on which equipment. Production scheduling aims to maximize the efficiency of the operation and reduce costs.
Production scheduling tools greatly outperform older manual scheduling methods. These provide the production scheduler with powerful graphical interfaces which can be used to visually optimize real-time work loads in various stages of production, and pattern recognition allows the software to automatically create scheduling opportunities which might not be apparent without this view into the data. For example, an airline might wish to minimize the number of airport gates required for its aircraft, in order to reduce costs, and scheduling software can allow the planners to see how this can be done, by analyzing time tables, aircraft usage, or the flow of passengers.
Companies use backward and forward scheduling to allocate plant and machinery resources, plan human resources, plan production processes and purchase materials.
Forward scheduling is planning the tasks from the date resources become available to determine the shipping date or the due date.
Backward scheduling is planning the tasks from the due date or required-by date to determine the start date and/or any changes in capacity required.
The benefits of production scheduling include:
- Process change-over reduction
- Inventory reduction, leveling
- Reduced scheduling effort
- Increased production efficiency
- Labor load leveling
- Accurate delivery date quotes
- Real time information
Contents |
Productivity
Productivity is the relation between quantity of inputs and quantity of output.
Inputs
Inputs are plant, labor, materials, tooling, energy and a clean environment.
Outputs
Outputs are the products produced in factories either for other factories or for the end buyer. The extent to which any one product is produced within any one factory is governed by transaction cost.
Within the factory
The output of any one work area within the factory is an input to the next work area in that factory according to the manufacturing process. For example the output of the cutting room is an input to the sewing room.
For the next factory
By way of example, the output of a paper mill is an input to a print factory. The output of a petrochemicals plant is an input to an asphalt plant, a cosmetics factory and a plastics factory.
For the end buyer
Factory output goes to the consumer via a service business such as a retailer or an asphalt paving company.
Resource allocation
Resource allocation is assigning inputs to produce output. The aim is to maximize output with given inputs or to minimize quantity of inputs to produce required output.
Scheduling Algorithms
Production scheduling can take a significant amount of computing power if there are a large number of tasks. Therefore a range of short-cut algorithms (heuristics) (a.k.a. dispatching rules) are used:
Stochastic Algorithms
Heuristic Algorithms
Batch Production Scheduling
Background
Batch production scheduling is the practice of planning and scheduling of batch manufacturing processes. See Batch production. Although, scheduling may apply to traditionally continuous processes, such as refining [1][2], it is especially important for batch processes such as those for pharmaceutical active ingredients, biotechnology processes and many specialty chemical processes [3][4]. Batch production scheduling shares some concepts and techniques with finite capacity scheduling which has been applied to many manufacturing problems [5]. The specific issues of scheduling batch manufacturing processes have generated considerable industrial and academic interest.
Scheduling in the Batch Processing Environment
A batch process can be described in terms of a recipe which comprises a bill of materials and operating instructions which describe how to make the product. [6] The ISA S88 batch process control standard [7] provides a framework for describing a batch process recipe. The standard provides a procedural hierarchy for a recipe. A recipe may be organized into a series of unit-procedures or major steps. Unit-procedures are organized into operations, and operations may be further organized into phases.
The following text-book recipe [8] illustrates the organization.
- Charge and Mix materials A and B in a heated reactor, heat to 80C and react 4 hours to form C.
- Transfer to blending tank, add solvent D, Blend 1hour. Solid C precipitates.
- Centrifuge for 2 hours to separate C.
- Dry in a tray dryer for 1 hour.
A simplified S88-style procedural organization of the recipe might appear as follows:
- Unit Procedure 1: Reaction
- Operation 1: Charge A & B (0.5 hours)
- Operation 3: Blend / Heat (1 hour)
- Operation 4: Hold at 80C for 4 hours
- Operation 5: Pump solution through cooler to blend tank (0.5 hours)
- Operation 5: Clean (1 hour)
- Unit Procedure 2: Blending Precipitation
- Operation 1: Receive solution from reactor
- Operation 2: Add solvent, D (0.5 hours)
- Operation 3: Blend for 2 hours
- Operation 4: Pump to centrifuge for 2 hours
- Operation 5: Clean up (1 hour)
- Unit Procedure 3: Centrifugation
- Operation 1: Centrifuge solution for 2 hours
- Operation 2: Clean
- Unit Procedure 4: Tote
- Operation 1: Receive material from centrifuge
- Operation 2: Load dryer (15 min)
- Unit Procedure 5: Dry
- Operation 1: Load
- Operation 2: Dry (1 hour)
Note that the organization here is intended to capture the entire process for scheduling. A recipe for process-control purposes may have a more narrow scope.
Most of the constraints and restrictions described by Pinedo[9] are applicable in batch processing. The various operations in a recipe are subject to timing or precedence constraints that describe when they start and or end with respect to each other. Furthermore, because materials may be perishable or unstable, waiting between successive operations may be limited or impossible. Operation durations may be fixed or they may depend on the durations of other operations.
In addition to process equipment, batch process activities may require labor, materials, utilities and extra equipment.
Cycle-Time Analysis
In some simple cases, an analysis of the recipe can reveal the maximum production rate and the rate limiting unit. In the process example above if a number of batches or lots of Product C are to be produced, it is useful to calculate the minimum time between consecutive batch starts (cycle-time). If a batch is allowed to start before the end of the prior batch the minimum cycle-time is given by the following relationship [10]:
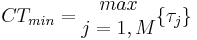
Where CTmin is the shortest possible cycle time for a process with M unit-procedures and τj is the total duration for the jth unit-procedure. The unit-procedure with the maximum duration is sometimes referred to as the bottleneck. This relationship applies when each unit-procedure has a single dedicated equipment unit.
If redundant equipment units are available for at least one unit-procedure, the minimum cycle-time becomes:
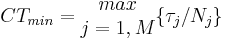
Where Nj is the number of redundant equipment for unit procedure j.
If equipment is reused within a process, the minimum cycle-time becomes more dependent on particular process details. For example, if the drying procedure in the current example is replaced with another reaction in the reactor, the minimum cycle time depends on the operating policy and on the relative durations of other procedures. In the cases below, and increase in the hold time in the tote can decrease the average minimum cycle time.
Visualization
Various charts are used to help schedulers visually manage schedules and constraints. The Gantt chart is a display that shows activities on a horizontal bar graph in which the bars represent the time of the activity. Below is an example of a Gantt chart for the process in the example described above.
Another time chart which also sometime called a Gantt chart[11] shows the time during which key resources, e.g. equipment, are occupied. The previous figures show this occupancy-style Gantt chart.
Resources that are consumed on a rate basis, e.g. electrical power, steam or labor, are generally displayed as consumption rate vs time plots.
Algorithmic Methods
When scheduling situations become more complicated, for example when two or more processes share resources, it may be difficult to find the best schedule. A number of common scheduling problems, including variations on the example described above, fall into a class of problems that become very difficult to solve as their size (number of procedures and operations) grows[12].
A wide variety of algorithms and approaches have been applied to batch process scheduling. Early methods, which were implemented in some MRP systems assumed infinite capacity and depended only on the batch time. Such methods did not account for any resources would produce infeasible schedules.[13]
Mathematical programming methods involve formulating the scheduling problem as an optimization problem where some objective, e.g. total duration, must be minimized (or maximized) subject to a series of constraints which are generally stated as a set of inequalities and equalities. The objective and constraints may involve zero-or-one (integer) variables as well as nonlinear relationships. An appropriate solver is applied for the resulting mixed-integer linear or nonlinear programming (MILP/MINLP) problem. The approach is theoretically guaranteed to find an optimal solution if one exists. The disadvantage is that the solver algorithm may take an unreasonable amount of time. Practitioners may use problem-specific simplifications in the formulation to get faster solutions without eliminating critical components of the scheduling model. [14]
Constraint programming is a similar approach except that the problem is formulated only as a set of constraints and the goal is to arrive at a feasible solution rapidly. Multiple solutions are possible with this method.[15][16]
Notes
- ^ Marcus V. Magalhaes and Nilay Shah, “Crude Oil Scheduling,” Foundations of Computer-Aided Operations (FOCAPO) 2003,pp 323-325.
- ^ Zhenya Jia and Marianthi Ierapetritou, “Efficient Short-Term Scheduling of Refinery Operation Based on a Continuous Time Formulation,” Foundations of Computer-Aided Operations (FOCAPO) 2003, pp 327-330
- ^ Toumi, A., Jurgens, C., Jungo, C., MAier, B.A., Papavasileiou, V., and Petrides, D., “Design and Optimization of a Large Scale Biopharmaceutical Facility using Process Simulation and Scheduling Tools,” Pharmaceutical Engineering (the ISPE magazine) 2010, vol 30, no 2, pp 1-9.
- ^ Papavasileiou, V., Koulouris, A., Siletti, C., and Petrides, D., “Optimize Manufacturing of Pharmaceutical Products with Process Simulation and Production Scheduling Tools,” Chemical Engineering Research and Design (IChemE publication) 2007, vol 87, pp 1086-1097
- ^ Michael Pinedo, Scheduling Theory, Algorithms, and Systems,Prentice Hall, 2002,pp 1-6.
- ^ T. F. Edgar, C.L. Smith, F. G. Shinskey, G. W. Gassman, P. J. Schafbuch, T. J. McAvoy, D. E. Seborg, Process Control, Perry’s Chemical Engineer’s Handbook, R. Perry and D. W. Green eds.,McGraw Hill, 1997,p 8-41.
- ^ Charlotta Johnsson, S88 for Beginners, World Batch Forum, 2004.
- ^ L.T. Biegler, I. E. Grossman and A. W. Westerberg, Systematic Methods of Chemical Process Design, Prentice Hall, 1999 p181.
- ^ M. Pinedo, 2002, pp 14-22.
- ^ Biegler et al. 1999, p187
- ^ M. Pinedo, 2002, p430
- ^ M. Pinedo, 2002, p28
- ^ G. Plenert and G/ Kirchmier, 2000, pp38-41
- ^ C. Mendez, J. Cerda, I. Grossman, I. Harjunkoski, M. Fahl, State of the art Review of Optimization Methods for Short Term Scheduling of Batch Processes, Computers and Chemical Engineering, 30 (2006), pp 913-946
- ^ I. Lustig, Progress in Linear and Integer Programming and Emergence of Constraint Programming, Foundations of Computer-Aided Operations (FOCAPO) 2003, 133-151
- ^ L. Zeballos and G.P. Henning, A Constraint Programming Approach to the Multi-Stage Batch Scheduling Problem, Foundations of Computer-Aided Operations (FOCAPO), 2003, 343-346
Additional References
- Blazewicz, J., Ecker, K.H., Pesch, E., Schmidt, G. und J. Weglarz, Scheduling Computer and Manufacturing Processes, Berlin (Springer) 2001, ISBN 3-540-41931-4
- Herrmann, Jeffrey W., editor, 2006, Handbook of Production Scheduling, Springer, New York.
- McKay, K.N., and Wiers, V.C.S., 2004, Practical Production Control: a Survival Guide for Planners and Schedulers, J. Ross Publishing, Boca Raton, Florida. Co-published with APICS.
- Pinedo, Michael L. 2005. Planning and Scheduling in Manufacturing and Services, Springer, New York.
See also
External links
- University of Nottingham. Inter-disciplinary Scheduling Network Research groups, scheduling link directories and a directory of scheduling suppliers.